hxb 2021 crypto
signin
$n1/n2$ 的连分数展开是对 $q1/q2$ 的一个逼近,所以枚举连分数中的每一项,就可以得到 $q1, q2$ 了,分解之后正常进行 RSA 解密得到 flag。
from Crypto.Util.number import GCD, inverse, long_to_bytes, isPrime
pk = (1150398070565459492080597718626032792435556703413923483458704675295997646493249759818468321328556510074044954676615760446708253531839417036997811506222349194302791943489195718713797322878586379546657275419261647635859989280700191441312691274285176619391539387875252135478424580680264554294179123254566796890998243909286508189826458854346825493157697201495100628216832191035903848391447704849808577310612723700318670466035077202673373956324725108350230357879374234418393233, 1242678737076048096780023147702514112272319497423818488193557934695583793070332178723043194823444815153743889740338870676093799728875725651036060313223096288606947708155579060628807516053981975820338028456770109640111153719903207363617099371353910243497871090334898522942934052035102902892149792570965804205461900841595290667647854346905445201396273291648968142608158533514391348407631818144116768794595226974831093526512117505486679153727123796834305088741279455621586989)
c1, c2 = (361624030197288323178211941746074961985876772079713896964822566468795093475887773853629454653096485450671233584616088768705417987527877166166213574572987732852155320225332020636386698169212072312758052524652761304795529199864805108000796457423822443871436659548626629448170698048984709740274043050729249408577243328282313593461300703078854044587993248807613713896590402657788194264718603549894361488507629356532718775278399264279359256975688280723740017979438505001819438, 33322989148902718763644384246610630825314206644879155585369541624158380990667828419255828083639294898100922608833810585530801931417726134558845725168047585271855248605561256531342703212030641555260907310067120102069499927711242804407691706542428236208695153618955781372741765233319988193384708525251620506966304554054884590718068210659709406626033891748214407992041364462525367373648910810036622684929049996166651416565651803952838857960054689875755131784246099270581394)
n1, n2 = pk
e = 0x10001
def getRoot(x, n):
high = 1
while high ** n <= x: high *= 2
low = high // 2
while low < high:
mid = (low + high) // 2
if low < mid and mid**n < x:
low = mid
elif high > mid and mid**n > x:
high = mid
else:
return mid
return mid + 1
# https://github.com/pablocelayes/rsa-wiener-attack
def rational_to_contfrac(x, y):
a = x // y
pquotients = [a]
while a * y != x:
x, y = y, x - a*y
a = x // y
pquotients.append(a)
return pquotients
def convergents_from_contfrac(frac):
convs = []
for i in range(len(frac)):
convs.append(contfrac_to_rational(frac[0:i]))
return convs
def contfrac_to_rational(frac):
if len(frac) == 0:
return (0, 1)
num = frac[-1]
denom = 1
for _ in range(-2, -len(frac) - 1, -1):
num, denom = frac[_] * num + denom, num
return (num, denom)
frac = rational_to_contfrac(n1, n2)
convergents = convergents_from_contfrac(frac)
p1, p2 = None, None
for (P1, P2) in convergents:
gcd1, gcd2 = GCD(P1, n1), GCD(P2, n2)
p1 = gcd1 if (gcd1.bit_length() <= 128 and isPrime(gcd1)) else p1
p2 = gcd2 if (gcd2.bit_length() <= 128 and isPrime(gcd2)) else p2
print(f"[+]p1: {p1}")
print(f"[+]p2: {p2}")
q1, q2 = getRoot(n1 // p1, 4), getRoot(n2 // p2, 4)
phi1 = (p1 - 1) * (q1 - 1) * q1**3
phi2 = (p2 - 1) * (q2 - 1) * q2**3
m1 = pow(c1, inverse(e, phi1), n1)
m2 = pow(c2, inverse(e, phi2), n2)
flag = (long_to_bytes(m1) + long_to_bytes(m2)).decode()
print(f"[~]flag: {flag}")
'''
[+]p1: 181856133933383097933223133658050179553
[+]p2: 196443958511498599913330690975430421229
[~]flag: flag{8ef333ac-21a7-11ec-80f1-00155d83f114}
'''
fastOT
Python 的random的内部是MT19937 伪随机数生成器,虽然生成的随机数周期很大,但是内部状态(state)很少,仅仅有 624 个,每个值都是 32bit 的。
这题给了足够的交互次数,题目中选项 1 里生成的m列表刚好是 8 个 32bit 的随机数,所以如果每次都能得到m列表,那么只需要交互 $624/8=78$ 次就可以得到全部的内部状态了,然后就能回推前面的随机数了。primate_key就是在前面生成的随机数。
为了得到m,需要对发送的内容构造一下,我们期望返回的结果也就是解密的结果对我们来说是已知的,服务端会对我们的消息分别用 $d_1, d_2$ 进行解密,所以发送的消息可以是 $c = m^{e_1\cdot e_2} \bmod n$,$m$ 可以是任意的已知明文,这样 $d_1$ 解密后的是 $c_2 = m^{e_2} \bmod n$,$d_2$ 解密后的是 $c_1 = m^{e_1} \bmod n$,$c_2, c_1$ 都是已知的,那么只需要异或一下就能得到m列表了。
有了所有的内部状态,也同样可以预测后面的值,每次的cur_rand都可以预测出来了,那么就可以解密得到flag。
from hashlib import sha256
from Crypto.Util.number import *
from Crypto.Cipher import AES
from tqdm import tqdm
from pwn import *
r = remote("127.0.0.1", "9999")
e1, e2 = 65537, 92431
msg = 1175078221
def unshift(value, key, mask=None, nbits=32, direction="right"):
maxn = (1 << nbits) - 1
if not mask:
mask = (1 << (nbits + 1)) - 1
i = 0
if direction == 'right':
while i * key < nbits:
part_mask = ((maxn << (nbits - key)) & maxn) >> (i * key)
value ^= ((value & part_mask) >> key) & mask
i += 1
return value
elif direction == 'left':
while i * key < nbits:
part_mask = ((maxn >> (nbits - key)) & maxn) << (i * key)
value ^= ((value & part_mask) << key) & mask
i += 1
return value
else:
raise ValueError("Invalid direction: %s, direction must be 'left' or 'right'." % direction)
def getState(number):
number = unshift(number, 18, direction="right")
number = unshift(number, 15, mask=0xefc60000, direction="left")
number = unshift(number, 7, mask=0x9d2c5680, direction="left")
number = unshift(number, 11, direction="right")
return number
def backtrace(numbers):
assert(len(numbers) == 624)
state = []
for number in numbers:
state.append(getState(number))
return state
def getOldStates(states):
for i in range(3, -1, -1):
tmp = states[i + 624] ^ states[i + 397]
if tmp & 0x80000000 == 0x80000000:
tmp ^= 0x9908b0df
res = (tmp & 0x40000000) << 1
tmp = states[i - 1 + 624] ^ states[i + 396]
if tmp & 0x80000000 == 0x80000000:
tmp ^= 0x9908b0df
res |= 1
res |= (tmp & 0x3fffffff) << 1
states[i] = res
def add(x, y):
assert y.bit_length() >= 128
return (x + y) ^ (x >> 53)
def get_m(message):
m0_list, m1_list = [], []
m0, m1 = int(message[0]) ^ pow(msg, e2, n), int(message[1]) ^ pow(msg, e1, n)
for _ in range(4):
m0_list.append(m0 & ((1 << 32) - 1))
m0 >>= 32
m1_list.append(m1 & ((1 << 32) - 1))
m1 >>= 32
m0_list.reverse()
m1_list.reverse()
return m0_list + m1_list
def choice_1():
r.sendlineafter(b'choice>', b'1')
r.sendlineafter(b"\n", hex(pow(msg, e1 * e2, n))[2:].encode())
r.recvuntil(b"Your message is (")
message = r.recvline().decode().strip()[:-2].split("L, ")
return get_m(message)
def choice_2():
r.sendlineafter(b'choice>', b'2')
r.sendlineafter(b"\n", hex(pow(msg, e1, n))[2:].encode())
r.recvuntil(b"Your cipher is: ")
return r.recvline().decode().strip()
def get_datalist():
datalist = []
for _ in tqdm(range(78)):
datalist += choice_1()
assert len(datalist) == 624
return datalist
r.recvuntil(b"Your pubkey is: ")
n = int(r.recvline().decode().strip().replace('L', '')[2:], 16)
print(f"[+] n: {n}")
datalist = get_datalist()
states = [0] * 4 + backtrace(datalist)
getOldStates(states)
random.setstate(tuple([3, tuple(states[:624] + [0]), None]))
primate_key = random.getrandbits(128)
print(f"[+] primate_key: {primate_key}")
for _ in range(624): random.getrandbits(32)
c = choice_2()
print(f"[+] cipher is: {c}")
t = (pow(pow(msg, e1, n), e1, n), pow(pow(msg, e1, n), e2, n))
cur_rand = random.getrandbits(128)
cur_k = t[cur_rand & 1] ^ cur_rand
key = sha256(long_to_bytes(add(primate_key, cur_k))).digest()[:16]
aes = AES.new(key, AES.MODE_ECB)
flag = aes.decrypt(bytes.fromhex(c)).decode()
r.close()
print(f"[~] flag: {flag}")
hxb 2020 crypto
古典美++
在 https://www.guballa.de/vigenere-solver 上解密,得到 key 是orderby。
from hashlib import md5
print(md5(b"ORDERBY").hexdigest())
得到flag:c82bbc1ac4ab644c0aa81980ed2eb25b
简单的密码3
only admin can get flag
Menu:
1) login
2) edit
3) flag
交互一下可以发现能修改iv,并且发送的用户名会和name:一起拼起来并加密,结合only admin can get flag可以猜测,如果解密后是name:admin就可以得到 flag 了,直接登陆 admin 也是不行的,只能通过修改iv来改变解密结果。
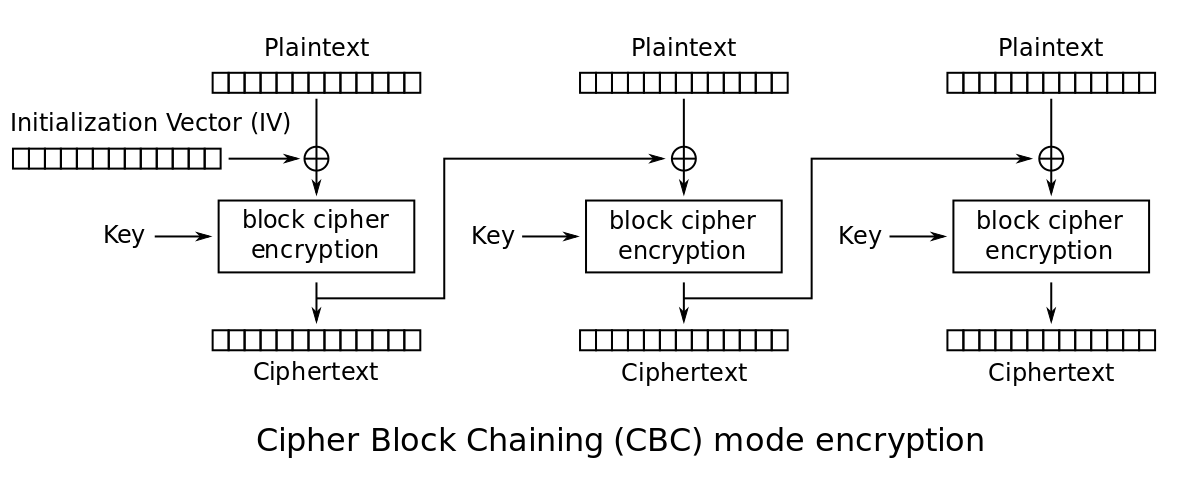
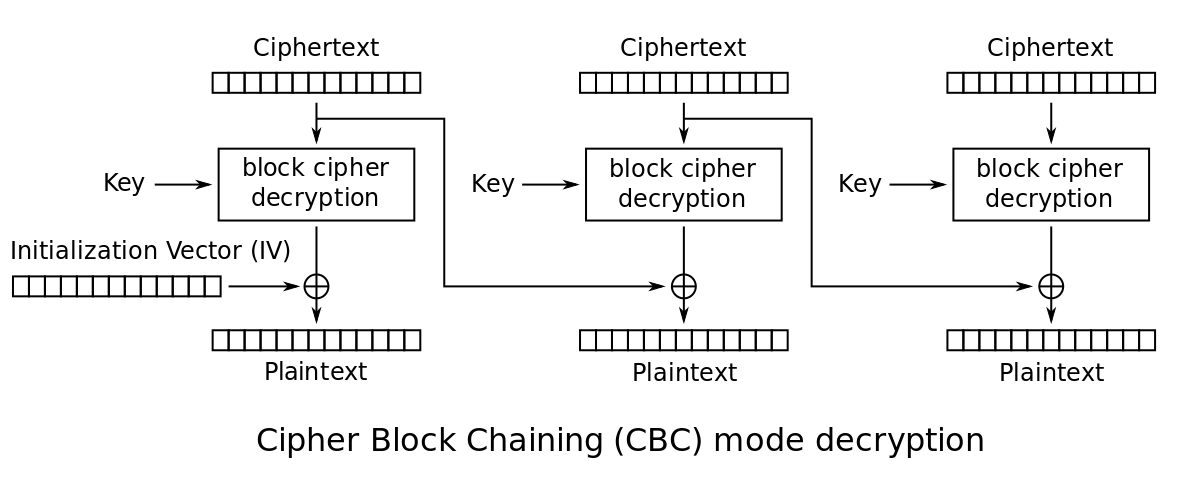
这里只需要观察解密过程最左侧的一块即可,密文经过key的解密后,异或iv,得到明文。
如果我们设置的用户名为1234567890,我们可以用name:1234567890异或当前的iv,得到key解密后的中间量,然后异或我们期望的明文name:admin即可。
newiv = iv ^ "name:1234567890" ^ "name:admin"
from Crypto.Util.number import *
iv = ""
iv = bytes.fromhex(iv)
def xor(x, y):
return b''.join([long_to_bytes(x[i] ^ y[i]) for i in range(len(x))])
def pad(x):
return x + long_to_bytes(16 - len(x)) * (16 - len(x))
payload = pad(b"name:admin")
plaintext = pad(b"name:1234567890")
# newiv = iv ^ plaintext ^ payload
print(xor(xor(iv, plaintext), payload).hex())
LFSXOR
明文是由长度为512字节的随机字符串和flag拼接起来的。加密脚本使用两个不同的 LSFR,分别生成了k4、k5两个密钥,并将用它们分别加密这同一段明文。
枚举全部的 k4 和 k5 的组合
pylfsr是一个可以自定义反馈函数的 lfsr 伪随机数生成器,L4和L5分别是定义在 $f = x^4 + x^3 + 1$ 和 $f = x^5 + x^4 + x^2 + x +1$ 上的 LFSR,初始状态都是随机的,周期分别为 15 和 31(因为全为 0 的状态不允许出现,所以是 $2^k-1$),初始状态也是 15 或 31 个中的其中一个。
由于它们周期都很小,初始状态也完全可以枚举,$15\cdot 31$ 种情况很容易爆破,对于每一组确定的初始状态,可以开始用它来生成 $k_4,k_5$,一共只有 $15\cdot 31$ 组 $k_4,k_5$,但是问题在于加密之前又将 $k_4, k_5$ 乱序了,所以接下来要想办法恢复 $k_4,k_5$ 正确的顺序。
获取乱序后的 k4 和 k5
可以利用前面提到的,乱序后的 $k_4,k_5$ 最终被用来加密同一段明文了,进行的是异或操作,所以对于一个字节的密文:
$$c_{1i} = k_{4i} \oplus m_i \ c_{2i} = k_{5i} \oplus m_i$$
所以可以利用 $c_{1i} \oplus k_{4i} = c_{2i} \oplus k_{5i} = m_i$ 来缩小当前位置是正确字节的可能,因为对于 $k_4$ 中的随机一个字节 $k_{4i}$ 和 $k_5j$ 中的随机一个字节 $k_{5k}$,刚好能异或对应位置 $c_{1i}, c_{2i}$ 得到相同结果的可能性并不高,在这个很小的范围中依次取一组信任,继续往下递归,直到这组 $k_4, k_5$ 一直可以满足条件,那么就用它们来解密。
from Crypto.Util.number import *
from pylfsr import LFSR
enc1 = b'\xbb\xd3\x08\x15\xc6:\x08\xb2\xb2\x9f\xe4p\xc7\xec\x7f\xfd)\xf6f\x9c\xe4\xd12\xaeJ\x81\xb1\x88\xab\xa5V\xa9\x88\x14\xdf`~\xf6\xdbJ\xb4\x06S!0\xbb\xe4\x1a\xe6R\x8e\x84X\x19K\x95\x07C\xe8\xb2\'\xa9\x80\x15\xec\x8f\x8dY\nK\x85\x99\xb7!\x134\xa9\xb6\x15\xcf&\r\x9b\xe1\x99\xe4]3h~\xf0\xa9\xa5\x14\xee}\xd19l\x14h\x07v *a0\x12\x14\xfe\x0f\x05\xdem\x1d\xe4s2J\x7f\xc28\xf6RR\x8e\xba\xb2m\x18M\xf1\xef!4\x17\xa8\xb4\x14\xc2\x8f\xb9Y:K\xaa\x06T!\x1b\xbb\xfd\xf6Gv\x8e\x9a\xeb\xd9K\xbb\x06N\x9a\x82c\xa9\xa0\x14\xed!\x04\xdbm\x13\xe5w3B\x7f\xd0\xa9\xbf\xb7\x9c\xe3\xd00\x83K\x86\xab3\x7f\xc1\xbb\xfd\x11\x15\xdf\x8e\x80Y\x07\xd8\xe5]2m\xe9\xbb\xce`\x91o\x8f\x8cY!\x81\xe4J\x92\x8c\xa7T\x16E\x15\xf1WMY(\xb8[\x8e2y~\xcbM\x10\x15\xc7\x1fWY\x0cK\x87\xce\xe5 !b\xa8\x83\x14\xec6\xd1!\xc8\x905\xe52L\xf1\xba\xcf\n\x9d\x9d\xe7u\xadm\x06\xe4n2r\xd8\xba\xed\xf6\x7f\x9d\xd8\xd02m\x12G\x07Y\x89\x7f\xc0\xa8\xa4\x15\xe5\x043Y\x1eJ\xae\x07n\x94\x87\xbb\xcf_\x8d\x9d\xd1\x14Y,\x9e\xe5b\xd7\x8c\x7f\xf7\xa8\x8f\x14\xc7\x8f\xb3\xb6\xf1\x93\xe4O\xdd\xc4\xdb\xba\xf6!\x15\xfd.\xd1\x18\xcf\xf6\x03\xea2E\x7f\xe1\xa9\xa5\xfe\x9d\xc9\xd1;\xd9\xee\x05\x06z\xc8\xb2\xbb\xe2\xf7{JW4\xcdm\x1a\xe5U\x8d \x0f&\x14\x7f\xf6\x9d\xd4E\xbf\xc3\xdb\xe4L\xe1\xf7\x90\xbb\xdaZ\xf4\x9d\xd13\xb8m3\xe2D3o~\xf8H\xf6U*\x07lY\x03K\xab\x07~\xa3\x87\xbb\xc9\xf7sAQ\x08Y6J\x86\x07Y\xec\xf7\xbb\xc6s\x15\xc6\x7fEY\x02J\x95\x07Z \x11\xbb\xc6T\x15\xfc-\xd0\x06\xe6\x9f-\x07^ \x15\xbb\xccz\x14\xf3\x8f\x97\xd4l9t\x85\xe8\x8a\xbe\xbb\xf9\xf6f\x9d\xf2\xd19\xa2K\xb6\xcd\xcf\xf6~\xd5\xa9\xaa\x15\xd8\x8e\xb3\x81m9\xe4f\xb2!\x1e\xba\xd8s\xfd\x11\x08W\xa1l;\x01\x07_!\x11\xbb\xdd\xf6x\x9d\xf0\x17Y\x15\xfe\x02\xc7\xa0!.W\xa9\xa5\x8f\x9c\xe8\xd1\x12m\x04\xe5s3Q~\xdd\xa9\xa3\x15\xdb\x8f\xac\xaf\xec\xbb\x10\xde2_\xba\xba\xe8\xf6f.\x1e\xd1\x17l\x06\xe4U\xdd\xf0\xd6~\x0fA\x14\xcb\x8e\xb0Y\x1fJ\xb2\xe4\xb3!"\xba\xfeU\x14\xedY\xd0>l-~\x06P 1\xbb\xf2\xf6waD\xd1(m\x12`\x06@\xb6~\xfa\xa9\xb1\xb0\x9d\xfb\x18\xfbm&\xe4v2w\xce\xba\xcbo\xd5\x07\x11QX<J\xbd\xb22O\x7f\xd8x>\xc8\x9c\xd3\xd03\x9d\xb5\x1e\xd72S\xf2ry\xf1W\x9c\xc89Y\rK\x8f\xff\x8a\xe0\xb5{\xa9\xae\xb1\x9d\xdd\xd1=\xbeK\xa3\x06e!\x08\xba\xd2\xf6j\x9c\xf6\xd0\x0fl#\xe5o\xf5\xaa~\xc2\xa9\x99\x15\xea6\xd1:\xe7\xa8\xe4n\xbb \nV\xa9\x91\x14\xf9}\xd0!m/\xe5|2o\x81\xba\xf8\r\x14\xeb\tR\xc9\xec\xdd`\xbf\xc6\x81\xdfKXW\xb3o.%\xa9\xcd\xb9\x14\xfd\x97\x83\x8eO\n\x03\xb6iuu\xab\x9d\xbc\x15\xf4\xc3\xd6\xc1'
enc2 = b'p\xfd\x1ff\xcaB\xa5\xe6`\x87\xa8\x8ci\x855\x92O8P\xa5}^\xd8\xed\x1a\x88=c\xe0\x9f\xedq\xf8\xe1%\x7fX\xd2\xba\xbe\x03\xa8\x9a\x9c\x075\x98"\xca\xed\xa4C^\xc6.j\xec\xfa\x10\xa7\xd9\x01\x06\x87\x90f\xcc\xf6\x1b\x0c\xde\xcc,\xfb\xf0\xc74\x94\xcfj\x8ay\xd5\xd2`.@\xed\xc2\xd8!DSp\xf5\x12f\xf1\xf6#\x80\xbe\x16\xa8\xaeF\xd0\xd1\xd4\xad\xb9\xf7#\x16\x08\xb2[\x1a\x87\x8b\xa0\xfaEF\xbf\x86\x8b\x8c\x90\xa4\xd5\xfbcR\xe2W\x9c\n5\x8b\xcfQ"\xf2\x16\x10\xb2I\x1a\x88\x8b\x8cj\x16\xebp\xccS\xd2\x90\xa8|q\x05\xafq\xfa\xcaHE{\x1a\xba#\xfd\x17/\xb2L\x1a\x87\x8a\x90\xc9Dmp\xef\x0ef\xf2Z|S\x00R\xfc\x1c\x9d\n5\x84\xceS\xb0\xa4M_\xff\xb9\x1a\x8a\x1d\\\x98D\\p\xcb*f\xdcV\xd0\xd5Q\xec\x1a\xfa\xf0\x91\xa8\xd4\x8a\xca\x9c-\x17\x07\xb2_\xff\n\x8a\x83\xfb\xc2\x00\x10\x87\x83\xaeF\xf7#\xd4\xbe\'\xa9\x8a$IMp\x14\xe8\xc0\xa4z\xd1\xb2H\xe6e\x8b\xb0\xcf\xb1\x01<\x87\x88g\xc2Q|H\xbe9\xa9\xad\x9c#4\x8cl8I\x0c\x17$\xb3}\x1b\x94\x01:j7\x00;\x86\xbd\xd2i\xf6\x1a\xa4\'R\xf6?\x9c\x08\xe1\xd4\xab\xdd\x8f\xa4[_\xca/@\xed\xe86\xf7\x9c\x018i\x04\xc3\x90\xa8\xaa\x0c\xde\xf2\xa8\xba?\xf4\xd39\xce\\"\xfe\x16\x0cY/]\xed\xe9l\xce\xa5\x018o,g\xdb\xf7\x12\xdag\xb6=\xfa\xccHgk\xcfH\xbf\x18\x9e\xbd\xb3u\x8f\n$Hk\x0e\xd3\xa6i\xe1\x15=\x16}R]\xb3\xa8\x82\x9b\x0b4\x9a\xcf{\xc2\xa4V\xe8:\x93\x1a\x83\x8a\x97j\t\x82\x88\x86\x80f\xf6*\xa2\xd5\xbe\x08\xa9\x98\x9c#\xf8\\\xceV\xa7\xa5L\xae&/t\xec\xfb\xd9\x02Dnp\xe8Cf\xf0U}R4\x87a\xfb\xf0I_\xd4\xaa\xb4"\xca\x16\x18>/i}\t\x03\xc1\x84\x00!\x86\x93g\xed\xf7\x1d\xc3\xbf\x01c\x06KI[\xd5\x929g\xa4t\x87\xb2\\\x1b\x8d\x0b\xd9\x0bDp\xf5om\xe1\x16\x0e}|ZR\xc4\xfb\xf2H@\xd4\xa28\\c\x17&\x07\xc8\xda~\x8b\x88\x86DS\xeb\x87\x87f\xda\xf73\r\xcaS\xd9\xfa\xfaI`\xd5\x889^R\x97\xaeF\xf6\x1a\x92N\xd8*Er\xc3\x16\xe0)\x91\xba|_Q\x83\x00>;\xff5\x82\xceX"\xd7\x17\x08P\xae\x1a\xb1\x8a\x8f\xc9Ep\xa7\x86\x86g\xf6m|o\xbf\x1c\xa9\xa1\x9c+\xc9\x1e\xcfI#\xfc\x92^\xc1\xb8\x1b\xad\x8a\x9e\xceEu\xb8$\xe0\x0b\x90\x87}[\x0fS\xcab]\xd2\xaaU\xcfh"\xfc\xa2_\xdd/y<C\x05k\x18\x00\x1aw\x1e\x9cA\xf6\x0f\x80w\x83\xae\xb8\x9d\x0e\xdc\xd4\xaf9H\\\xaf\x9ey\xef\x1b\xb4.\xd99Dd\xa2\x87\xa7f\xc6\xf6\n\x0c\xc4R\xd7\xfa\xe4Hc\xd4\xa78Jc\x9c^\xca.u\xed\xfcak&\x8b\x92\x87\x88\xee\x90\x83\x90\x0c\xd9R\xcd\x08\x9c04\xb1\xceC"\xea\xe9^\xe3\xd4\x1a\x9a\x0c[\xfa\xc5\x97\xf5>\x15\xc71\x06\x8d\xac\x19\xa0\t\x0el\xe9\xc6%4\x9d\x80U\xe3\xfdF\x8d\xee\x17.+\x9b\xb3\xf0\x83w\x16\xd9'
enc1 = list(enc1)
enc2 = list(enc2)
# 如果候选随机顺序的密钥,和当前定好顺序的密钥 含有相同数量的相同字节Int,那么就需要排除掉这个字节,不需要再对这个字节进行处理
def counter(Lis1, Lis2, Int):
return sum([int(i == Int) for i in Lis1]) == sum([int(i == Int) for i in Lis2])
'''
对于每一次递归的开始,k4 k5被认定是正确的密钥,但是顺序不对
ir 是当前递归的深度(用于判断的第i个密文字节)
'''
def dfs(nk4, nk5, k4, k5, ir):
if ir == 300:
print("k4 =", nk4)
print("k5 =", nk5)
content = b''.join([long_to_bytes(nk4[i % len(nk4)] ^ enc1[i]) for i in range(len(enc1))])
print(content)
exit(0)
if len(nk4) < 15 and len(nk5) < 31:
for k4i in k4: # 15
if counter(nk4, k4, k4i):
continue
for k5i in k5: # 31
# 如果使用k4中的一个值 和 k5中的一个值和当前密文字节异或结果相同,那么可以继续往下递归
if (k4i ^ enc1[ir]) == (k5i ^ enc2[ir]):
if counter(nk5, k5, k5i):
continue
dfs(nk4+[k4i], nk5+[k5i], k4, k5, ir + 1)
return
if len(nk4) == 15 and len(nk5) < 31:
for k5i in k5:
if (nk4[ir % 15] ^ enc1[ir]) == (k5i ^ enc2[ir]):
if counter(nk5, k5, k5i):
continue
dfs(nk4, nk5 + [k5i], k4, k5, ir + 1)
return
if len(nk4) == 15 and len(nk5) == 31:
if (nk4[ir % 15] ^ enc1[ir]) == (nk5[ir % 31] ^ enc2[ir]):
dfs(nk4, nk5, k4, k5, ir + 1)
return
for i in range(2**4):
ini = [int(r) for r in list("0"*(4 - len(bin(i)[2:])) + bin(i)[2:])]
L4 = LFSR(fpoly=[4, 3], initstate=ini, verbose=True)
data = L4.runFullCycle()
k4 = b""
for _ in range(len(data)):
a = b''
for __ in range(8):
a += str(L4.next()).encode()
k4 += long_to_bytes(int(a, 2))
k4 = list(k4)
for ii in range(2**5):
iini = [int(r) for r in list("0"*(5 - len(bin(ii)[2:])) + bin(ii)[2:])]
L5 = LFSR(fpoly=[5, 4, 2, 1], initstate=iini, verbose=True)
data = L5.runFullCycle()
k5 = b""
for _ in range(len(data)):
a = b''
for _ in range(8):
a += str(L5.next()).encode()
k5 += long_to_bytes(int(a, 2))
k5 = list(k5)
dfs([], [], k4, k5, 0)
# DASCTF{7cc33bd1c63b029fa27a6a78f1253024}
Offline CTF (travel)
2021
密码正常 ak,signin 硬推了一会儿没想起用连分数,都被打烂了才交 flag;fastOT 三血,进了决赛。不过现在由于疫情,可能会去不成长沙。
线下赛:疫情,寄了
2020
线上赛密码ak,队友输出很猛,成功进决赛。
线下赛去了湖南,留影记念。




