这题使用的加密算法是 Demytko,属于一种类似 RSA 的在椭圆曲线上的加密算法,这题的攻击思路也是可以完全类比 RSA Hastad 广播攻击。
加密后的结果是椭圆曲线上的点, Division Polynomials 使我们可以用仅含一个未知数的多项式来表示这个点的 $x$ 坐标:
$$ \begin{aligned} \psi_{-1} &=-1 \\ \psi_{0} &=0 \\ \psi_{1} &=1 \\ \psi_{2} &=2 y \\ \psi_{3} &=3 x^{4}+6 a x^{2}+12 b x-a^{2} \\ \psi_{4} &=4 y\left(x^{6}+5 a x^{4}+20 b x^{3}-5 a^{2} x^{2}-4 a b x-8 b^{2}-a^{3}\right) \\ \psi_{2 i+1} &=\psi_{i}\left(\psi_{i+2} \psi_{i-1}^{2}-\psi_{i-2} \psi_{i+1}^{2}\right) / 2 y, i \geq 2 \\ \psi_{2 i} &=\psi_{i+2} \psi_{i}^{3}-\psi_{i+1}^{3} \psi_{i-1}, i \geq 3 \end{aligned} $$
此外,还可以定义多项式 $\phi_{m}$ 和 $\omega_{m}$:
$$ \begin{aligned} \phi_{m} &=x \psi_{m}^{2}-\psi_{m+1} \psi_{m-1} \\ \omega_{m} &=\left(\psi_{m+2} \psi_{m-1}^{2}-\psi_{m-2} \psi_{m+1}^{2}\right) / 4 y \end{aligned} $$
那么椭圆曲线上的数乘,就可以用 Division Polynomials 来表示了:
$$ m P=\left(\frac{\phi_{m}(P)}{\psi_{m}(P)^{2}}, \frac{\omega_{m}(P)}{\psi_{m}(P)^{3}}\right) $$
$$ ciphertext=\frac{\phi_{m}(P)}{\psi_{m}(P)^{2}} $$
$$ f=ciphertext\cdot \psi_{m}(P)^{2}-\phi_{m}(P)=0\ (mod\ n) $$
由于密文给了 $70$ 组,所以 $f_i$ 多项式一共有 $70$ 个,由于指数 $e=3$,所以 $f_i$ 为九次同余方程,可以通过中国剩余定理将 $70$ 个同余方程合并成一个,这时得到的是一个系数很大,模数 $N$ 也很大的九次同余方程,这时可以通过格基规约算法得到模这个很大的 $N$ 的意义下的、较小的系数,当真实系数小于 $N$ 时,同余方程便可以直接看作等号连接的方程,即可很方便的求解一个较小的根(明文)。
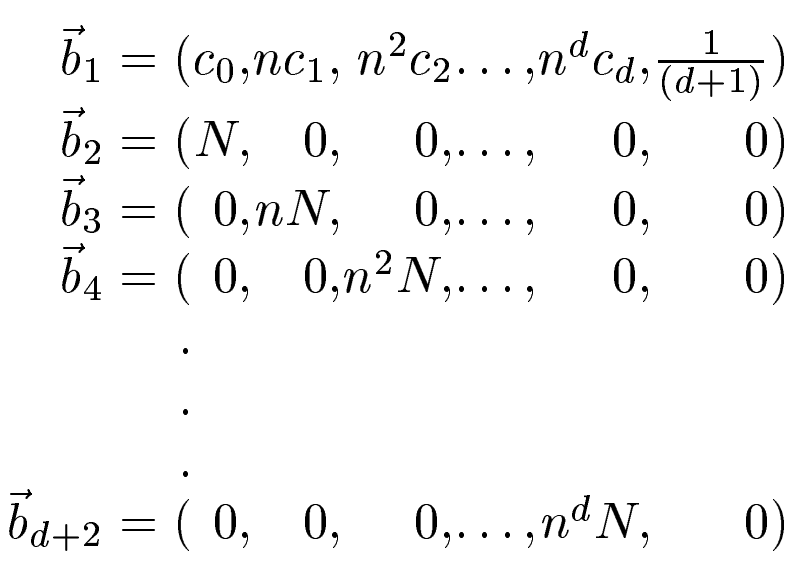
参考论文 SOLVING SIMULTANEOUS MODULAR EQUATIONS OF LOW DEGREE
非预期:在使用 CRT 合并成一个同余式之后,由于明文 $m$ 相对 $n$ 过于小,可以用 Sage 的
.small_roots求解出根,这样就不需要自己规约了。
from functools import reduce
from Crypto.Util.number import *
f = open("data", "r")
ciphertext = []
a, b, n = [], [], []
for i in range(70):
ci, ai, bi, ni = [int(num) for num in f.readline().strip().split(", ")]
ciphertext.append(ci)
a.append(ai)
b.append(bi)
n.append(ni)
e = 3
deg = 9
coeffi = []
for i in range(70):
E = EllipticCurve(IntegerModRing(n[i]), [a[i], b[i]])
P.<m> = PolynomialRing(Zmod(n[i]))
f = ciphertext[i]*E._multiple_x_denominator(e, m) - E._multiple_x_numerator(e, m)
coeffi.append(f.coefficients(sparse=False))
large_coeffi = [crt([int(coeffi[j][i]) for j in range(70)], [n[j] for j in range(70)]) for i in range(deg+1)]
N_bitlength = sum([n[i].bit_length() for i in range(70)])
min_n = min(n)
N = reduce(lambda x, y: x * y, n)
Sc = large_coeffi
var("x")
assume(x, 'integer')
f = Sc[9]*x^9 + Sc[8]*x^8 + Sc[7]*x^7 + Sc[6]*x^6 + Sc[5]*x^5 + Sc[4]*x^4 + Sc[3]*x^3 + Sc[2]*x^2 + Sc[1]*x + Sc[0]
lat = []
lat.append([large_coeffi[i]*min_n**i for i in range(deg+1)]+[1/(deg+1)])
for i in range(deg+1):
lat.append([((min_n**j)*N if (i==j) else 0) for j in range(deg+1)]+[0])
Mat = matrix(lat)
Mat_LLL = Mat.LLL()
for lin in range(deg):
Sc = [int(i) for i in Mat_LLL[lin]]
Sc = [(Sc[i] // (min_n**i)) for i in range(deg + 1)]
var("x")
assume(x, 'integer')
f = Sc[9]*x^9 + Sc[8]*x^8 + Sc[7]*x^7 + Sc[6]*x^6 + Sc[5]*x^5 + Sc[4]*x^4 + Sc[3]*x^3 + Sc[2]*x^2 + Sc[1]*x + Sc[0]
print(factor(f))
break
'''
m = 3088969433059681806521206959873975785377227976800172674306727155831805513908352148702210247662586117242206183337522557
print(long_to_bytes(m))
'''
Nep{LOoK_aT_th3_sT4R-Lo0k_h0w_tH3y_5h1N3_fOr_Y0u}